Tenth in a series with puzzle solving tips. This time with advice on Fillomino puzzles and hidden polyominoes.

Fillomino is one of my favorite puzzle styles, in part because it is one of the few where I think the author’s touch can come across in the puzzle in so many different ways. In the set of Fillominoes I’ve gotten from different authors, I think I can pick out some authors from others just based on how much they use visual patterns, one-option polyomino growth, crowding, counting, how well they conceal hidden pentominoes, and so on. While having a variety of puzzle constructors will improve most sections of The Art of Puzzles, Fillomino is hands-down in my mind the one where having many authors will have the greatest effect on quality.

I wanted to talk about one of my own constructing trends which I learned this week after writing 7 Fillomino puzzles (only a few that went online; some are going to GAMES and others are being saved). That is what I’ll call the “known unknowns”. The picture you should have in your head when considering a choice based on the hidden polyominoes you’ll leave behind. The contradictions in the “known unknowns” are the basis for the Saturday Fillomino.

Besides the lower-left corner, the deductions in this image come from looking just at the 2’s and considering leftovers. Not all may seem trivial so it will be worth figuring out how to get here. Basically, when you know you are stranding some cells as part of a hidden polyomino, they have actually have live options around them. With the 2’s (and the corner 1’s), these eliminations are hopefully simple enough.

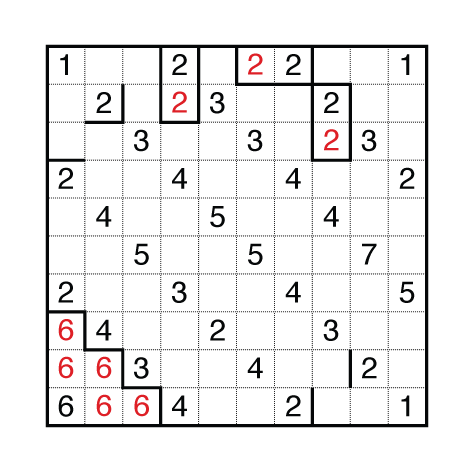
A little extra can be done along the top, but the key first break-through is in the upper-left. There is a “known unknown” hidden polyomino in that corner which will “start” at whichever cell the 2 clue does not use. It must be of size at least 3, starting in R1C2 or R2C1 as drawn in red.

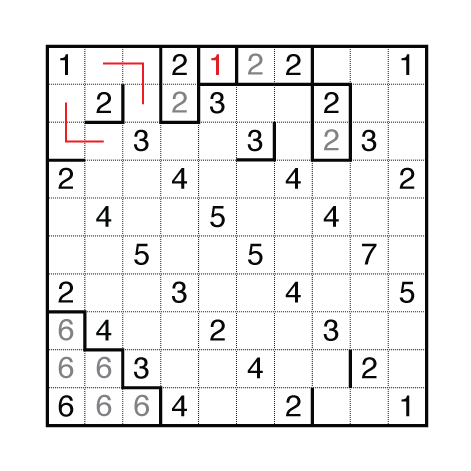
But if you consider the surrounding digits, it needs to be even larger than 3 so one of these is surely impossible. Marking off the other one, the hidden polyomino grows to size of at least 5 and a lot of other digits can be placed.

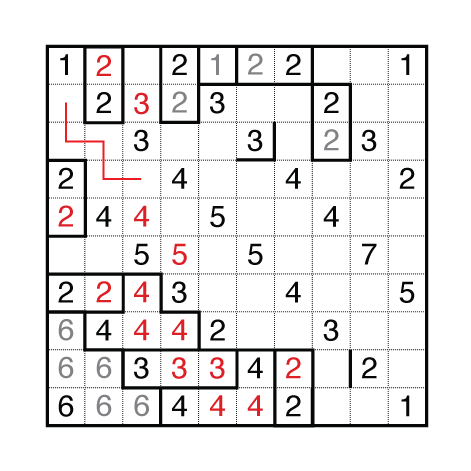
Here, there are now a few visualizations to convince yourself of only one option. Consider if the 5’s do not all connect in the middle. Can you squeeze them in and also fit in the 4’s? Then consider if the 4’s above them can connect or not. Leaving two unfilled cells on the left marks that as impossible too. These aren’t that complicated to spot but they get us to the next good discussion point.

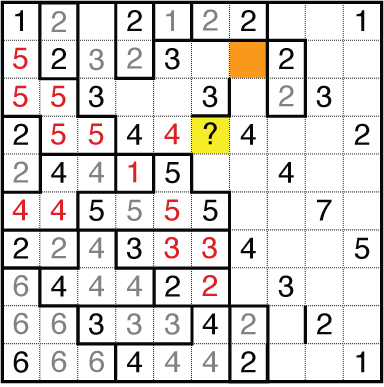
While we don’t know the number that goes in the orange cell, it must be either a hidden 1 or part of the 4 below. If the ? in yellow is connected to the 4, this leaves the known unknown of “1” in the orange cell, next to another 1 in the cell just beneath. That is a real no go. The ? must be some other digit but 4 and the rest of the top goes in pretty smoothly from crowding.

At this stage there are a couple options to resolve the right side, but one of the more interesting for this lesson starts at the top. Again, consider the cell in orange. We know it is not a 1 or a 2, so it must connect down at least one cell.

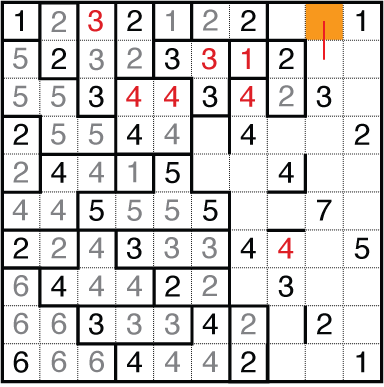
Consider what happens if it connects to the 3. We again leave a hole of two cells to the right, and the 1 and 2 around it keep it from being filled. So the red line marks another known unknown, of size 4 or 5, and putting in the forced conclusions from that gets the 3 to block a cell beneath it. While the 7 was somewhat crowded before, it is now very crowded logically and by figuring out how to grab enough cells you should easily make your way to the conclusion.

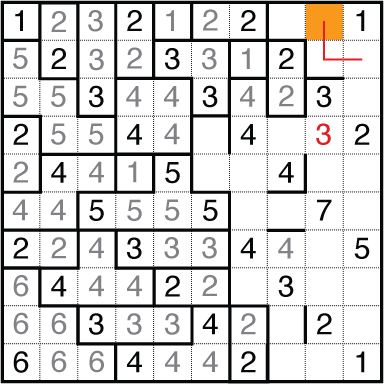
With Fillomino puzzles, knowing the author’s style may be half the battle. For my puzzles, it seems knowing where unknowns might go, and visualizing consequences with some either/or choices, will get you through the puzzle fast. One of my testers was on this wavelength. The others struggled. So it goes.