Round Trip by Craig Kasper
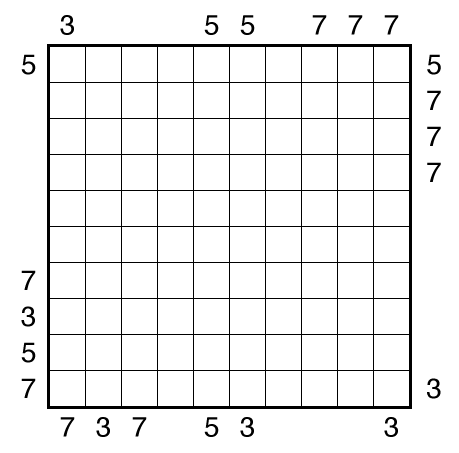
or solve online (using our beta test of Penpa-Edit tools; in default linex mode: left-click+drag draws line, right click marks X on edge)
Theme: Odd Lots
Author/Opus: This is the 7th puzzle from guest contributor Craig Kasper.
Rules: Draw a single loop in the grid which may cross itself orthogonally, but otherwise does not touch or retrace itself. The clue numbers to the left/right of the rows indicate the number of squares visited by the nearest section of the loop that travels horizontally in the rows. The clue numbers to the top/bottom of the columns indicate the number of squares visited by the nearest section of the loop that travels vertically in the columns.
Also, see this example:
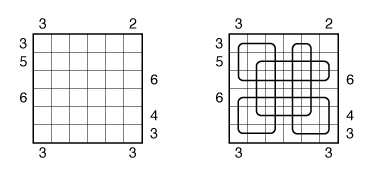
Answer String: Enter the number of empty squares for each row from top to bottom, followed by a comma, and then the number of turns for each row from top to bottom. This example has the key “100000,422224”.
Time Standards (highlight to view): Grandmaster = 3:30, Master = 5:00, Expert = 10:00
Solution: PDF; a solution video is available here.
Note: Follow this link for other Round Trip puzzles. Some more Round Trip puzzles can be found in the book Loop Variety Collection by Ashish Kumar and Murat Can Tonta.

I’m enjoying these puzzles. One thing I’m less wedded to is the answer key. I think I’d prefer the “ILX-” notation that Croco-Puzzle has been using for this sort of thing for a couple of key rows.
I have to agree with that, I *really* dislike the answer key format for these puzzles. Perhaps instead something more like what you use for Star Battle or Battleships would work better, ie column of first or second turn for each row, 0 if there are no horizontals.
– Neelix
These puzzles are great, but I’m having a real tough time working out my notation for tracking things mid-solve.
Wednesday I needed to differentiate “endpoint that definitely doesn’t extend” from “endpoint that maybe extends”. Today I need to differentiate “two-way intersection” from “two-way that might become four-way”.
I’ve been putting a “T” for the “endpoint that definitely doesn’t extend” and a plus for the “two-way that might become a four-way”. In both cares I erase or grey out the extra branches that don’t get used, turning either T or + into an L.
I have been doing well “X”ing the borders where I know the lines can’t cross to another cell (as on the opposite sides of lines drawn parallel with the grid border), and extending those X’s into adjacent cells that can by extension not make an + junction. That way, when I have a corner connection, I know if it can be a + or not if it has an X on a border or not. And if there are no X’s, I know that it simply might end up being a + junction.
I had to restart this one for some reason, but got it cleanly and quickly the second time through. I always enjoy Craig’s puzzles.
I agree with Vraal. Mark walls onto the cell edges that the path cannot cross, should fix both your differentiation issues.