Araf (Inequality) by Prasanna Seshadri
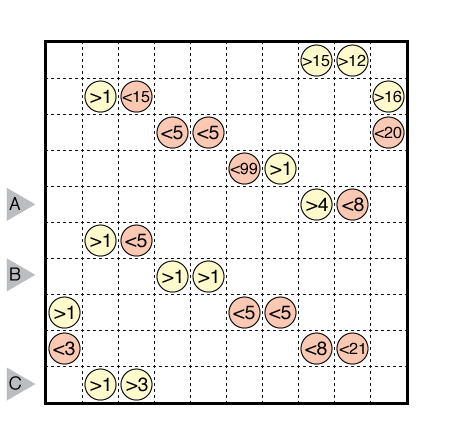
or solve online (using our beta test of Penpa-Edit tools; use tab to alternate between a composite mode for line/edge drawing and a shading mode.)
Theme: Clue Symmetry and Logic
Author/Opus: This is the 23rd puzzle from our contributing puzzlemaster Prasanna Seshadri.
Rules: Divide the grid into some regions formed of edge-adjacent squares. Each cell is part of one region, and each region should contain exactly two given numbers, one in a yellow circle (>) and one in a red circle (<). Each region must have an area that is strictly between those numbers. Answer String: Enter the number of cells in each connected group (between bold lines) in the marked rows. Separate the rows with a comma.
Time Standards (highlight to view): Grandmaster = 3:00, Master = 4:45, Expert = 9:30
Solution: PDF
Note: Araf is a relatively new puzzle for us on GMPuzzles. Follow this link for other Araf. An example image for a “classic” Araf puzzle is here.

Interesting connection logic on this one. For me, there are times when Araf feels like Fillomino, and times when it feels more like Numberlink. This one felt more like Numberlink.
I’m not sure how I feel about the Inequality style yet. One the one hand, good “classic” Araf can feel like elegant sleight of hand. The puzzles look like they can’t possibly be unique and then everything starts to come together. This style seems more predictable and logical in some ways, but there’s also something nice about being able to take a clue like the 15 and 16 up in the top corner and force them to be LOWER bounds.
Maybe I’m being dumb but I just now realized that the > and < actually mean greater than and less than. The way the instructions were worded I thought they just were there to identify the regions as being separate if you didn't have a color printout or something. I solved the one yesterday without that knowledge but I'd been looking at today's for a really long time and couldn't see any way to solve it without some major league guessing. I'm thinking now I might be able to get it.
02:28.
Great global logic stuff, nicely done.