PDF

or solve online (using our beta test of Penpa-Edit tools; use tab to alternate between a composite mode for line/edge drawing and a shading mode.)

Theme: Triplets

Author/Opus: This is the 78th puzzle from our contributing puzzlemaster Ashish Kumar.

Rules: Standard Spiral Galaxies rules.

Difficulty: 1.5 stars

Time Standards (highlight to view): Grandmaster = 0:50, Master = 1:20, Expert = 2:40

Solution: PDF; a solution video is also available here.

Note: Follow this link for classic Spiral Galaxies puzzles on this website and this link for variations on Spiral Galaxies puzzles. If you are new to this puzzle type, here are our easiest Spiral Galaxies Puzzles to get started on. More Spiral Galaxies puzzles can be found in The Art of Puzzles 2.

After many years of publishing elegant, hand-crafted puzzles across multiple genres in focused e-books and one-off collections, we have decided to start a more regular quarterly publication where every 3 months we will feature selections from six different categories of puzzles. Today marks the release of Grandmaster Puzzles Quarterly: Volume 1, which has 60 total puzzles split across these genres:

– 7 Sudoku and 3 Killer Sudoku
– 7 TomTom and 3 TomTom (Different Set)
– 7 Star Battle and 3 Star Battle (Isometric)
– 7 Tapa and 3 Tapa (Line)
– 7 Fillomino and 3 Fillomino (Non-consecutive)
– 7 Yajilin and 3 Yajilin (Regional)

We are already pretty far along in preparing volume 2, which will be even larger than the first volume, and we are continuing to consider additional features to put into this recurring series over time. So please try out this first volume, and then share any feedback you have so we can continue to make a great quarterly publication.

At the end of the year (at the release of volume 2), we expect to offer some options to subscribe to this series of books to receive them at a discount.

The recent mix of “Last Days of SUM-mer” arithmetic puzzles is collected in this PDF and the solutions are in this PDF.

The daily solution videos are on the posts and linked below:

This next week of puzzles will be themed around Spiral Galaxies puzzles.

We have recently added several more Penpa versions of puzzles to the site, completing the main entries for TomTom and LITS styles, to bring us to over 775 puzzles digitized so far this year. The six completed sudoku genres and six completed puzzle genres are listed on our Penpa Notes page.

Later today we’ll be posting the first issue of a new book series, Grandmaster Puzzles Quarterly 1. This book has 60 total puzzles, with six sections containing 7 “regular” puzzles and one variation with 3 more puzzles. The first issue focuses on Sudoku, TomTom, Star Battle, Tapa, Fillomino, and Yajilin. Each section is meant to resemble a full week of GMPuzzles on the web, but packed with extra content. While this first issue took more time than expected to prepare, our managing editor Serkan Yürekli and contributing authors are pretty far along with Grandmaster Puzzles Quarterly 2 which will be out by the end of the year with an even larger size.

PDF

or solve online (using our beta test of Penpa-Edit tools)

Theme: It’s T Time

Author/Opus: This is the 215th puzzle from our contributing puzzlemaster Prasanna Seshadri.

Rules: Standard Sudoku rules. Also, the sum of the digits in each cage must equal the value given in the upper-left corner of that cage. Digits cannot repeat inside a cage.

Difficulty: 4.5 stars

Time Standards (highlight to view): Grandmaster = 11:15, Master = 19:00, Expert = 38:00

Solution: PDF; a solution video is also available here.

Note: Follow this link for more Killer Sudoku and this link for classic Sudoku. More Killer Sudoku puzzles can be found in Killer Sudoku by Serkan Yürekli.

PDF

or solve online (using our beta test of Penpa-Edit tools; use tab to shift between number entry and shading modes.)

Theme: Magic Squares

Author/Opus: This is the 32nd puzzle from our contributing puzzlemaster JinHoo Ahn.

Rules: Place the digits in the indicated range (1-9) in some of the cells so that no digit is repeated in any row or column. Numbers on the outside of the grid indicate the sums of adjacent digit groups in that row or column, in order. Each sum is separated by at least one unused cell.

Difficulty: 4.5 stars

Time Standards (highlight to view): Grandmaster = 7:15, Master = 20:00, Expert = 40:00

Solution: PDF; a solution video is also available here.

Note: Follow this link for other Japanese Sums puzzles.

PDF

or solve online (using our beta test of Penpa-Edit tools)

Theme: Signed by the Author

Author/Opus: This is the 352nd puzzle from our contributing puzzlemaster Grant Fikes.

Rules: Standard TomTom rules, using the integers 1-5. The two grids have the same numerical clues in the cages with the given operations (e.g. the sum of the upper-left cage in the top grid equals the product of the upper-left cage in the bottom grid). The value of all mathematical operations must be nonnegative integers.

Difficulty: 3 stars

Time Standards (highlight to view): Grandmaster = 3:45, Master = 4:45, Expert = 9:30

Solution: PDF; a solution video is also available here.

Note: Follow this link for classic TomTom and this link for TomTom variations. If you are new to this puzzle type, here are our easiest TomTom to get started on. More TomTom puzzles can be found in the TomTom collection, in The Art of Puzzles, and in our beginner-friendly collection Intro to GMPuzzles by Serkan Yürekli.

PDF

or solve online (using our beta test of Penpa-Edit tools; use tab to shift between number entry and shading modes.)

Theme: Ten’s Complement

Author/Opus: This is the 206th puzzle from our contributing puzzlemaster Murat Can Tonta.

Rules: Fill each row and column of the grid with the digits 1 to 4 and two blackened cells. Numbers outside the grid indicate the sum of the digits between the two blackened cells in that row or column. Blackened cells are allowed to touch. Or see here.

Difficulty: 2.5 stars

Time Standards (highlight to view): Grandmaster = 2:15, Master = 3:00, Expert = 6:00

Solution: PDF; a solution video is also available here.

Note: Follow this link for other less common Number Placement puzzles.

PDF

or solve online (using our beta test of Penpa-Edit tools)

Theme: Sequence

Author/Opus: This is the 77th puzzle from our contributing puzzlemaster Ashish Kumar.

Rules: Variation of Skyscrapers; each clue represents the sum of the heights of the visible buildings in that direction.

Difficulty: 2 stars

Time Standards (highlight to view): Grandmaster = 1:30, Master = 2:00, Expert = 4:00

Solution: PDF; a solution video is also available here.

Note: Follow this link for classic Skyscrapers puzzles and this link for variations on Skyscrapers puzzles. If you are new to this puzzle type, here are our easiest Skyscrapers Puzzles to get started on. More Skyscrapers puzzles can be found in The Art of Puzzles, in our beginner-friendly collection Intro to GMPuzzles by Serkan Yürekli, and in the e-book Skyscrapers by Ashish Kumar.

PDF

or solve online (using our beta test of Penpa-Edit tools)

Theme: Crossing the River

Author/Opus: This is the 53rd puzzle from our contributing puzzlemaster Palmer Mebane.

Rules: Standard Kakuro Rules.

Difficulty: 1.5 stars

Time Standards (highlight to view): Grandmaster = 0:50, Master = 1:20, Expert = 2:40

Solution: PDF; a solution video is also available here.

Note: Follow this link for classic Kakuro and this link for Kakuro variations. More Kakuro puzzles can be found in Kakuro and Variations by Serkan Yürekli and in The Art of Puzzles 2.

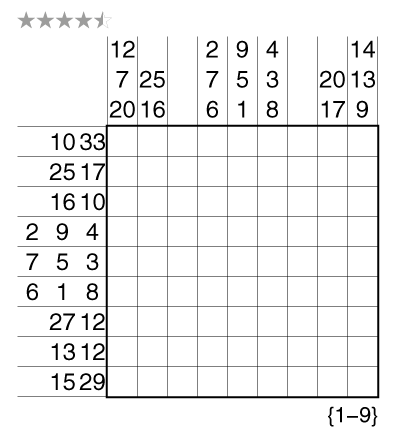
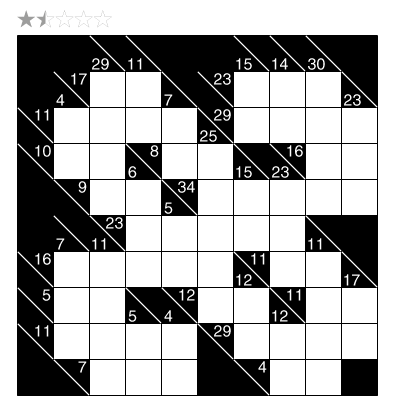
This year, we started posting some extra difficult Sunday Stumpers, about once a month. These will be quite tough puzzles, but with a logical path to be found (and solution videos to help). This eighth Sunday Stumper is a Hungarian Tapa from puzzlemaster Palmer Mebane.

(view directly for a larger image)

PDF

or solve online (using our beta test of Penpa-Edit tools)

Theme: Four Corners of Four

Author/Opus: This is the 52nd puzzle from our contributing puzzlemaster Palmer Mebane.

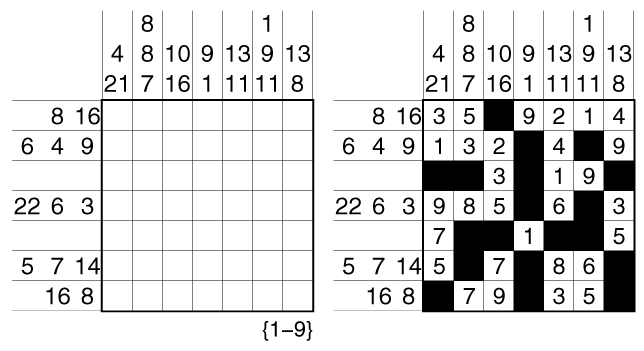
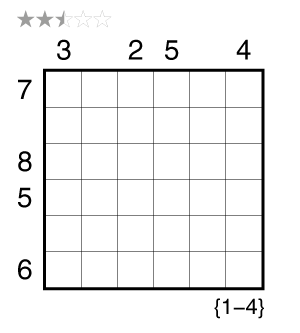
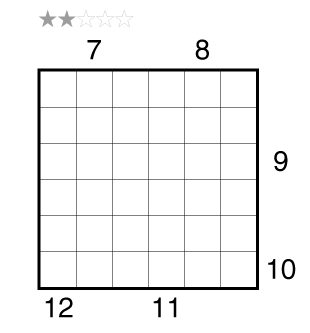
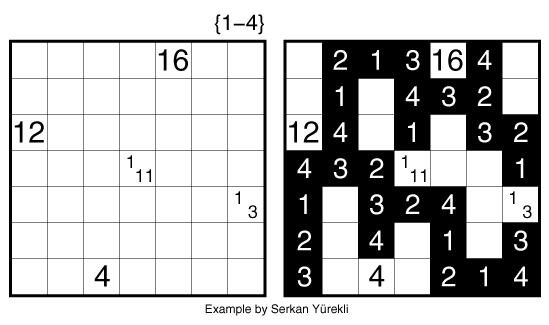
Rules: Variation of Tapa. Shade some empty cells black to create a single connected wall. Cells with numbers cannot be shaded, and the shaded cells cannot form a 2×2 square anywhere in the grid. Each row and column must contain eight shaded cells (four for the example). Place a number from 1 to 8 (1-4 for the example) into each shaded cell so that each number appears once in each row and column.

Numbers in a cell indicate the sums of the numbers of consecutive shaded blocks in the neighboring cells. If there is more than one number in a cell, then there must be at least one white (unshaded) cell between the black cell groups. Numbers on the shaded cells can repeat in a sum.

See also this example:

Difficulty: 5 stars

Time Standards (highlight to view): Grandmaster = 35:00, Master = 1:05:00, Expert = 2:10:00

Solution: PDF; a solution video is also available here.

Note: Follow this link for classic Tapa and this link for Tapa variations. If you are new to this puzzle type, here are our easiest Tapa puzzles to get started on. More Tapa puzzles can be found in The Art of Puzzles, in Tapa and Variations, and in our beginner-friendly collection Intro to GMPuzzles, all by Serkan Yürekli.