Star Battle by Thomas Snyder
or solve online (using our beta test of Penpa-Edit tools)
Theme: Star Frame (prepared for the 2017 Puzzle Grand Prix)
Author/Opus: This is the 270th puzzle from Thomas Snyder, aka Dr. Sudoku.
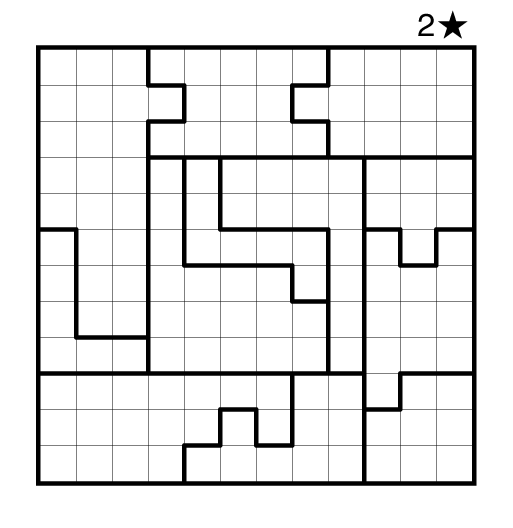
Rules: Standard Star Battle rules. Two stars per row, column, and region.
Answer String: For each row from top to bottom, enter the number of the first column from the left where a star appears. Enter these numbers as a single string with no separators.
Time Standards (highlight to view): Grandmaster = 2:30, Master = 5:15, Expert = 10:30 (*Estimates from competition scoring, not our usual process)
Solution: PDF
Note: Follow this link for other classic Star Battles. If you are new to this puzzle type, here are our easiest Star Battles to get started on. More Star Battle puzzles can be found in The Art of Puzzles.

2:44.Lovely & fun puzzle.I liked the size(12X12)and would love to see more of 12X12 SBs on GMP.
This one is crushing us. I’ve marked only 12 squares where stars cannot go and have not placed any stars. What are we missing?
This one is a bit tricky, but it comes down to the geometry. Think about the outer frame that surrounds the 6×6 square and how all of those outer regions have to work together. I can give a more direct hint if you are still stuck.
I’m just struggling where to start with this starbattle could you give more direct hint please
You want to look at the outer groups of three rows (1,2,3 and 10,11,12) and three columns (1,2,3 and 10,11,12). There are three regions only in columns 10,11,12 for example which should give you two easy stars in a fourth region that is partially in this space. Conversely, the first three rows only have three regions in them in total, so all the other cells coming down the left side cannot contain stars as that would keep six stars from appearing in rows 1, 2, and 3.
This puzzle heavily uses the count of regions in the outer frame like the two examples above.