Araf by Serkan Yürekli
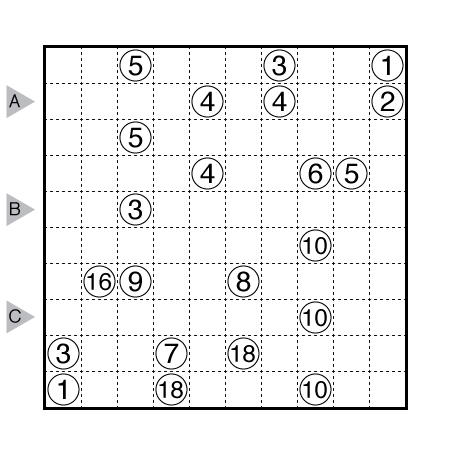
or solve online (using our beta test of Penpa-Edit tools with a composite mode for line/edge drawing.)
Theme: Clue Symmetry
Author/Opus: This is the 27th puzzle from our contributing puzzlemaster Serkan Yürekli.
Rules: Divide the grid into some regions formed of edge-adjacent squares. Each cell is part of one region, and each region should contain exactly two given numbers. Each region must have an area that is strictly between those numbers (This means, for two number clues A and B with A < B, the area C fulfills A < C < B).
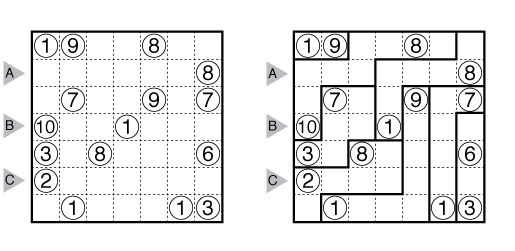
Answer String: Enter the number of cells in each connected group (between bold lines) in the marked rows. For the example above, this is “34,121111,4111”.
Time Standards (highlight to view): Grandmaster = 4:00, Master = 6:15, Expert = 12:30
Solution: PDF
07:09.
Every step of this puzzle is amazing. The opening begins with a wonderful distant connections that forces most of the puzzle, and the ending is beautiful extremities play. Great puzzle.
Very interesting Araf. I don’t think I have seen one that opens or ends like this before.
so was the intended ending step gb pbhag znkvzhzf?
Marvelous puzzle, a delightful solve. Thanks 🙂
I was very scared of this puzzle when it was announced, because it feels a bit reminiscent of Numberlink, which requires as much intuition as it does logic. But this was a very doable, enjoyable puzzle.
Just to make sure, I guess “Each region must have an area that is strictly between those numbers” means that the number of squares in a region must be between the two givens but not equal to those numbers.
So an region containing the numbers 1 and 4 must contain 2 or 3 squares.
In other words : b is STRICTLY between a and c means a < b < c (or c < b < a) where b is between a and c could be a <= b <= c (or c <= b <= a).
Do I understand this correctly ?
Yes. You can always check your understanding with the example; if it’s not strict, R4C7 (along with some other cells) are ambiguous.
I’ve put this clarification into the rules above. I don’t know why I shy away from mathematical formalism at times but I think the inequalities above will now be clear.
Thanks !
I absolutely loved the forcing logic of this puzzle. It was
such a pleasure to watch the solution unfold. Thanks for the fun.