The Puzzle Robot #15 – The Persistence of Memory
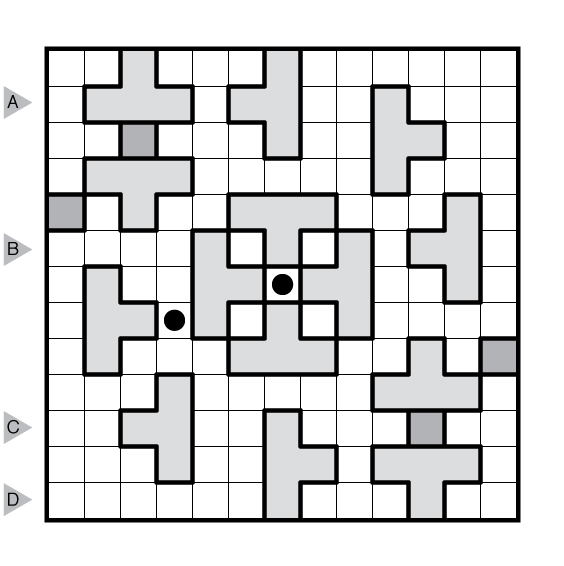
(View image directly for larger form.)
(PNG with extra lines for solvers who want to flood-fill the path)
or solve online (using our beta test of Penpa-Edit tools using a composite mode where left click inside cell shades square, left click + drag draws line segment, right click inside cell adds dot, and right click on cell edge adds an x.)
Theme: T
Rules: Find a path from one dot to the other by moving horizontally or vertically between adjacent squares. The path cannot touch itself, even diagonally. All highlighted regions must be used, and may be re-entered. If two or more highlighted regions have the same shape and orientation, then how the path passes through those shapes must be identical. Or see here.
Answer String: For each marked row, enter the size of each group of cells used by the path from left to right. Separate each row’s entry with a comma.
Time Standards (highlight to view): Grandmaster = 2:45, Master = 5:30, Expert = 11:00
Solution: PDF

The rule that states that path squares cannot otherwise touch each other, not even diagonally is confusing. Where the path makes a right angle, the path squares will definitely touch diagonally. So when is it not okay for path squares to touch?
As a biochemist, I want to make an analogy to protein structure and that the rule is about avoiding tertiary interactions from distant parts of the chain. But I don’t know if that picture will work for you.
Anyway, the rule (as seen in almost all snake puzzles) is meant to prevent the path from doubling back near itself. If you number the path squares from 1 to N, there would never be two path squares whose difference is >2 that touch, even diagonally.
Thanks for asking the question Andy and thanks for the good answer Thomas. I’ve always sort of understood that the rule was meant to prevent doubling back but was never 100% sure if a random zigzag was or wasn’t legal and how officially to tell. The difference > 2 rule makes for an easy determination.