Sunday Surprise #7 – Welcome to Serkan Yürekli
Editor’s Note: While our Sunday Surprises are meant to be unexpected, today’s surprise should be a double surprise for you. Besides the bonus puzzle, it is my great pleasure to announce that one of the world’s best puzzlemakers and the inventor of Tapa, Serkan Yürekli, is joining us as a regular contributor. (If you haven’t yet, you should check out his Tapa Variation Contests that are starting again this weekend and his Classic Tapa Contest that starts next week.)
I asked Serkan, for his debut week, to provide some of the puzzle styles I know him best for and I hope you will enjoy what is in store. Today brings a “The Persistence of Memory” puzzle that Serkan wrote with GMPuzzles in mind.
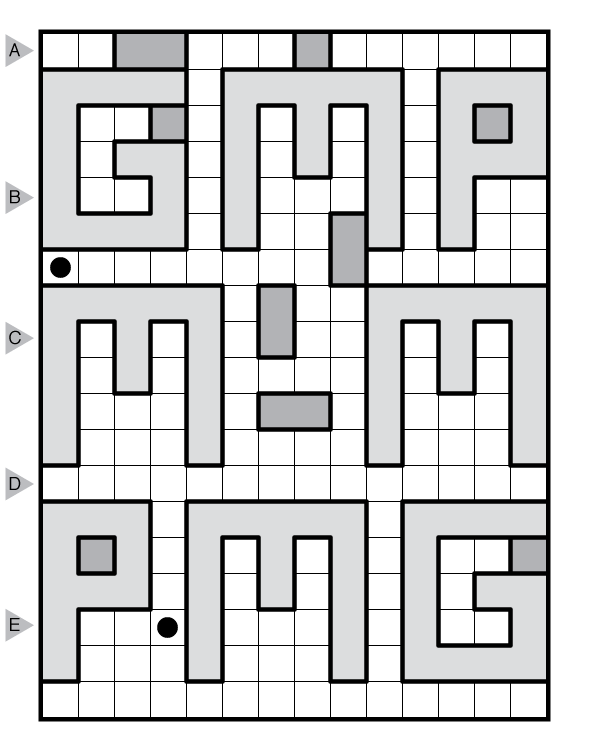
(View image directly for larger form.)
(PNG with extra lines for solvers who want to flood-fill the path)
or solve online (using our beta test of Penpa-Edit tools using a composite mode where left click inside cell shades square, left click + drag draws line segment, right click inside cell adds dot, and right click on cell edge adds an x.)
Theme: GMPuzzles
Rules: Find a path from one dot to the other by moving horizontally or vertically between adjacent squares. The path cannot touch itself, even diagonally. All highlighted regions must be used, and may be re-entered. If two or more highlighted regions have the same shape and orientation, then how the path passes through those shapes must be identical. Or see here.
Answer String: For each marked row, enter the size of each group of cells used by the path from left to right. Separate each row with a comma.
Time Standards (highlight to view): Grandmaster = 7:30, Master = 10:30, Expert = 21:00
Solution: PDF

Well, one thing for sure is that the shaded regions should still have the grid lines so that floodfilling the squares passed by the path (which is unique due to the no-touching rule) is possible. Only my opinion though; if everyone else solves The Persistence of Memory by drawing the path and not shading the squares passed, then okay.
I broke the puzzle heh. I’ll try it again later.
We used an art style like we’ve seen before from Serkan for this type. I made another png for floodfillers which you can use if you try it again.
I appreciate the flood-fill version. Also very happy to see Serkan on board.
This one was a good challenge. Definitely one of those puzzles where you work little bits and pieces and then the whole thing snaps together rather suddenly.
Also, I will add my recommendation to the Tapa from Serkan over at LMI. I did a pretty mediocre job on this TVC test, but I really enjoyed the puzzles (even if I had to do most of them later). And the first CTC is still one of my favorites — lots of variety within a single type, and elegant designs.
Are two regions not considered “identical” if one is highlighted and the other isn’t? Otherwise I don’t see how the 1×2 boxes in the top left can be filled.
Only the highlighted regions follow that rule (I’ve added the word highlighted a second time into the rules for clarity).
Every white cell or group of white cells should be treated independently and may or may not be used.
Very nice puzzle!
And welcome Serkan, that is a nice surprise!
Step one: Stare at the puzzle blankly.
Step two: re-read the rules carefully, and go look at examples to make sure you understand them.
Step three: slowly start making deductions, gaining confidence as you go, and working path logic into the solve once your deductions have given you the critical mass to do so.
Step four: Finish solving the puzzle, and smile.
Serkan certainly has gotten his contributions off to a very nice start.
I’m very happy to see this puzzle! I have enjoyed the USPC Persistence of Memory puzzles and I’m looking forward to more contributions.
(I have no idea what “floodfilling” is, or why I would need to explicitly see the gridlines in order to do it.)
(That’s for solvers you are doing the puzzles on their computer instead of on paper. It is using Paint or similar program and just filling the whole cell when it is or isn’t used.)
10:31.Took me 9 years to solve this : )