From the Foxger’s Den #42: Statue Park
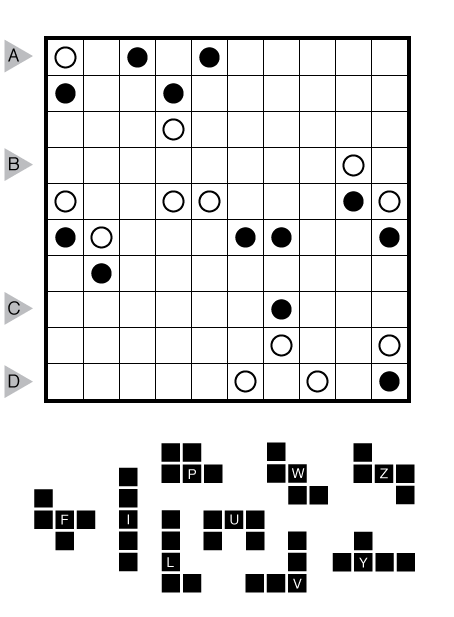
or solve online (using our beta test of Penpa-Edit tools)
Theme: Antisymmetry!
Rules: Standard Statue Park rules. The given subset of the pentominoes is to be used in this puzzle, with rotations and reflections allowed.
Answer String: Enter the length in cells of each of the shaded segments from left to right for the marked rows, starting at the top. Separate each row’s entry from the next with a comma.
Time Standards (highlight to view): Grandmaster = 2:30, Master = 3:45, Expert = 7:30
Solution: PDF
Note: Follow this link for other Statue Park Puzzles. If you are new to this puzzle type, here are our easiest Statue Parks to get started on.

Is the correct step in the middle of the solve “svthevat bhg jurer gur V zhfg tb”, or is there another way to go at it?
I think that’s the key step — you can do it pretty early on and everything after that snaps into place quickly.
It was in fact “too easy” after that step that I had to ask whether I was actually making a logical deduction, or whether that was guessing.
Well, it’s definitely logical. You do a bit of early straightforward stuff near all the givens, and then if your pentomino radar goes off and you ask where that one piece goes, it’s really easy to prove that there’s only one way to do it. Mind you, I wouldn’t be surprised if the solving times were pretty bimodal, depending on how quickly the penny dropped for each solver. Still, I think developing good instincts about what you ought to be looking for is an important part of getting good at puzzle solving, and this is a good little lesson.
03:48 crap. Spent about 20 seconds staring because I think there are more possible solutions and I accidentally break a rule somewhere.
A nice puzzle. I think my crucial step in the middle was “these four pieces are all LPYZ so the rest are the remaining left”, which put one pentomino. Only after that I saw a solution (I didn’t realize the I was forced at that point). After that, give the 20 seconds of thinking the U might be placed in a different orientation and making me think I broke somewhere (apparently not).
Antisymmetry and wonderful solving path. Can you make an antisymmetric puzzle with all pentominoes in? 😉