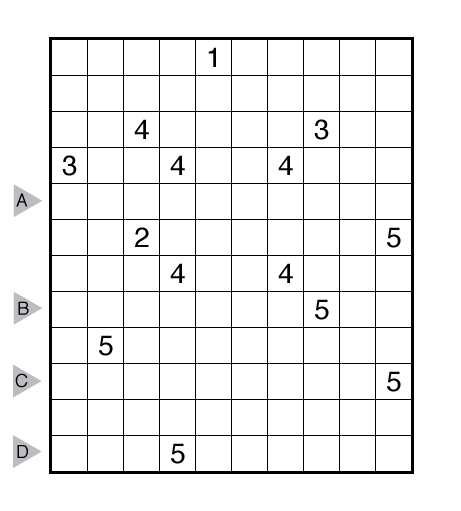
Dr. Sudoku Prescribes #77 – Nurikabe (Unique Islands)
or solve online (using our beta test of Penpa-Edit tools)
This is a “Twisted Tuesday” puzzle variation.
Theme: Unique Islands
Rules: Standard Nurikabe rules. Also, each island shape must be unique. This means that no two islands, including rotation and/or reflection of the shapes, can be superimposed.
Answer String: Enter the length in cells of each of the black segments (the unnumbered, connected “ocean”) from left to right for the marked rows, starting at the top. Separate each row’s entry from the next with a comma.
Time Standards (highlight to view): Grandmaster = 4:15, Master = 6:00, Expert = 12:00
Solution: PDF

Great puzzle, but, … boy, did “I #$%&* the bed” on that one. 17 minutes +.
I didn’t work the limited 4-cell options at first, then after I got through those, I forgot about 2 of the 5-cell options.
Great piece of puzzle construction though, and very enjoyable despite my own defects.
Thanks.
TheSubro.
Nice puzzle. I had to run some combos, but nothing that I needed scratch work for.
So, to poke the dragon, why does shape uniqueness work here but you don’t think string-uniqueness will work well in a Seek-and-Spell variant?
Lots of reasons, including how “natural” a constraint feels, and how strongly limiting it is. Great puzzles have few constraints but the constraints mean a lot. No repeated shapes means a lot and affects almost all placements here — the 3s and the 4s and even the 5s meaningfully at the end. It is THE focus of this variation on a familiar tableau of Nurikabe.
The concern that the same digits might sit kitty-corner on a box edge of a sudoku and give two paths in a seek-and-spell variant cannot be a major part of that puzzle. The Seek-and-Spell rule itself is THE focus, and it does not need an extra “meta” requirement. I certainly can’t construct a puzzle in that variant of a variant where path uniqueness comes up enough to be worth the rule. And the deductions I’m imagining that could stem from it are much more indirect and at times probably needlessly unfair. It seems a little more like an inelegance than a benefit.
I could take a broken sudoku with two solutions and add the rule “the string 4129 does not occur in consecutive adjacent cells” to make it have one. It wouldn’t be a big part of the solve, but that one time you use it would be critical to getting the one solution.
But I’d rather never ever have to add such a silly rule. I’m not saying “string uniqueness” is as insane as “4129”. But my view of the expected value of either rule in any puzzle is about the same — close to zero. It can only be an add-on and not the main course.
One other reason I believe it works well for this puzzle is very much the “Polyomino” aspect of the solve. Its a concept that when understood helps for many other puzzle types, e.g. the potential shape of a certain area.
By taking a few seconds and making a quick sketch of the possible Polyomino’s below the puzzle for each number, I probably saved myself a few minutes easily of trying to keep them in mind and searching during the solve.
Whereas the “Seek & Spell” Sudoku variant, while an enjoyable puzzle, doesn’t really have many additional techniques that apply to other puzzle types. Adding additional unique conditions may make a good one time puzzle, but I agree that it sort of feels like fixing a “broken” puzzle.
I don’t even really see this as a uniqueness constraint though. It’s just a rule borrowed from pentomino/tetromino puzzles, where you can’t use a shape more than once. Even Battleships has this constraint in a way, as you always get a given fleet.
I see these as set constraints, where you are limited to a set of shapes to place and you can’t use any shape more than you are given.
A loop/path uniqueness constraint is never directly given though in any type. It’s inferred by puzzle rules to get a unique solution when the solution will be the loop or path and it has to look the same as what the solver will get.
But in Seek and Spell and its variants, your solution will be a grid of letters/numbers/symbols. As long as the solution of letters and numbers will look the same on your paper as in the solution that the constructor had in mind, then path uniqueness is irrelevant. You will still end up with the correct solution.
In the end, the whole point of puzzling is that the constructor ensures that you get the same solution as intended, as this is the only one possible with the given constraints. And sometimes this means uniqueness inferrences can apply, but other times this isn’t necessarily the case.
22:57
5:00. I liked the top half. The 4’s were nice and constraining( though I had to get back to the top 4 after I realized a bit into the solve it has to be an ‘O’).I struggled with the two 5s in the bottom-right for sometime, but recovered soon.
03:48.
An interesting variation. There are a few sticking points, but the 5s at bottom-right are the one that gives me the most trouble. Took me some time to realize that one of them can be a P-pentomino.
That was great! I loved the way the 4s came together especially. The 5s seemed a little bit more of the feeling of solving a system of simultaneous equations to figure out which pentominoes I needed and which ones I could use where, like it was pushing the limits of what I could keep in my head without trial-and-error.