Ask Dr. Sudoku #12 – The line must be drawn here
To [guess], or not to [guess], that is the question:
Whether ’tis Nobler in the mind to suffer
The [Twists] and [the Turns] of outrageous [Logic],
Or to take Arms against a Sea of troubles,
And by [guessing] end them….
We’ve had a fair number of lively discussions in the last week, and if nothing else has come out of them at least the comment threading on the site is now noticeably improved. One question that has come up a lot has been around which puzzles need guesswork, here and elsewhere. A lot of solvers, for the sake of speed perhaps, will say they “had to bifurcate” during a solve here, but that has never been required for our puzzles. This week I wanted to (briefly) state my opinions on what I consider to be “logical” puzzles, since I mention frequently that all puzzles will have a single solution that can be reached by logic alone and it is worth contributors and solvers knowing what I mean by that.
My background is in experimental science, so my answer is going to be a practical one: When I can solve a puzzle in ink, without erasures, with all deductions either positive or negative coming from visualization in my head and not making scratch-work on the paper, the puzzle is solvable by logic.
That’s it. While a mathematical argument may talk about how some steps come about as an indirect proof (consider situation A; if so then B and C but C is not possible for other reasons, so not A) and most indirect proofs are indeed a trial-and-error process, this is allowed within the “pen” definition if I can keep the entire trial in my head to see the result. On the other hand, when the necessary trials are particularly involved, and I can only make it to the finish by using a branched search with underlined numbers or different colors or eventually lots of erasing, and certainly when I can reach a solution and not know it is the only one, that puzzle requires guesswork. The pen versus pencil test is the one I always have in mind.
So my standard is an organic one, unfortunately tied to my abilities as a solver and therefore hard to codify, except most experienced solvers will be able to see the same moves I can and there will be general agreement on what is logical. This standard is the right one for me as a puzzle publisher because it is tied to my solvers’ expected experience with the puzzles and what will seem “fair.”
But there is a broader discussion that often gets entangled with the first, practical one. Which is “do we know enough heuristics of any type to solve this particular puzzle logically?” The deepest knowledge base is certainly in sudoku, and a lot of well-annotated solution software is out there such as the SudokuWiki solver. Last I checked, somewhere around 0.5% of all randomly generated minimal sudoku will not be solvable by SudokuWiki using any of the steps it lists (and you must remove all the uniqueness rectangle steps when running this test as you are doing logical steps, not meta-logical steps). Some people might hope to discover new tricks, such as with entangled threads or new combinations of strong and weak links or other group theoretic constructs to further “solve” the sudoku problem. So that 0.1% or 0.01% or eventually 0% of sudoku remain “unsolvable.” As a puzzler, I am completely uninterested. Let me explain:
Despite all the steps listed on SudokuWiki, many of them are exclusively computation-friendly steps. Many of them are searches that are functionally so deep or across such a large search space that a human will not practically ever find them. I’m much more interested in how Kasparov plays chess than Deep Blue, even if the question of solving the game of chess so White always wins will be done by the latter. Computers solving chess will not fundamentally change how humans (using just their brains) will play the game. Similarly, there will be no set of deductions that will make all sudoku be solvable by me as a human. The number of “fair” puzzles is probably just 90% of all randomly generated minimal puzzles, maybe even less.
To me, no heuristic in orange or below on the SudokuWiki solver is a proper step to include in a puzzle given to a human solver. And only some of the yellow steps, when presented in the right context, are good. “Simple Colouring” is probably the worst of these as it is very much an “eliminate candidates by holding two guesses in your head” kind of process. And oftentimes when colouring works, the reason to choose that particular number and those two particular branches is not a natural one. I’d keep X-wings and swordfish and place the Y-wing on the edge as the line beyond which my sudoku puzzles will not cross. And when I do include them, I mean to have them stand out as proud examples of the step that fit organically into the solve and not just as something that happens to resolve the last 15 digits where most solvers will lack the patience and randomly guess.
This was effectively the starting picture I wanted solvers to get to on Saturday’s puzzle:
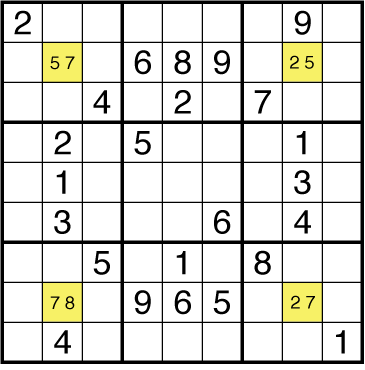
Sure, there are 5 digits that can be gotten more easily. And then a few pairs to identify. But fundamentally this puzzle was constructed to have a Y-wing required early in a telegraphed place – the four symmetric bi-value cells in yellow. The original grid shape was going to be a big circle with a slash in it: A visual “Do Not Guess” warning. But to get to one solution it took some tweaking from the original theme.
If you’ve never reasoned out before why a 7 cannot go into R8C2, this may feel like guesswork. The Y-wing step, while mathematically solid in a sudoku language of strong and weak links, feels like guesswork until you get used to seeing it. The Y-wing is where I draw the line. And when the World Sudoku Championships pushed the envelope far past this line, making me and all other solvers have to guess instead of think to win championships, I stopped having interest in competing at the WSC. I had to not just be sure to use pencil, but also bring extra erasers, and this is not the experience I would be having if the clock weren’t involved.
So while my solvers may frequently say they guessed on a puzzle — even I would if I were solving some of these at a competition — none of the puzzles we post here will require you to guess, at least in writing. You may need to do a little mental trial-and-error to figure out the next step forward, but that is all. Just as on Friday’s Tapa, the eliminations such as those around the “5 1” clue on the left, can be comfortably done without looking too far forward if you know to look for them at all. This doesn’t mean our puzzles can’t be very hard. It just means you should be able, without the clock in mind, to engage in a fair fight with the puzzle and however long it takes feel victorious at the end. This total victory over the puzzle is the joy that comes from persevering through a hard battle. And it cannot be offered if you need to guess and can’t be sure you’ve won.

Great writeup. Very glad to start to understand your approach on these. Of course, I’m still hurting my brain looking a couple of the other puzzles you linked to from the other discussion, which brings me to this question: How long do you think a relative novice should continue to fight the good fight before seeking help either from other individuals or a solver like the one linked to? Certainly there is satisfaction to finally finding the key, but I figure if someone gets to the point of saying “Well, let’s try this and see what happens”, you’ve lost the chance to actually learn a technique.
The first time you discover some of these steps it will most often be from guessing/intuiting that there is a particular problem that is constraining some area. So hoping to visualize it all without some help may not be possible.
One of my forthcoming projects, at least for Sudoku, is a book that talks about how to solve these puzzles and identifies many of the hard steps. I’d present them first with a “Just One Cell Sudoku” form where in about 8-12 givens I can show you how the rule pops up. Then in another few example puzzles you can see in progressively harder places how to spot the same rule. In the absence of a good tutorial, it can be a struggle for awhile to get good at Swordfish and other steps as they are quite challenging compared to most of the sudoku steps you generally use — at least until you have a lot of practice with them.
As an experienced solver, I feel the same. When I solve for fun I always like to solve by pen, just to force the logic far more than I would in speed solving. There’s numerous genres that might fair quicker with a good guess, but I think by not making that guess solving when still learning, it helps when you find the logic involved and maybe teaches you to recognise it the next time you encounter a similar step. I haven’t had to do anything I would call a guess to get through any puzzle on the blog.
I think for anyone trying to get faster in the beginning it’s far more important to understand the logic better than to solve as fast as possible. I feel it’s far more useful to find the required logic first. And once you have that, you can try to find ways to also help quick intuitive guesses to maybe speed up the solve. I understand it can sometimes be frustrated to not be able to see that one step, but it’s more useful to eventually find the required logic.
I have to disagree with you on simple colouring. Some of Wei-Hwa’s best puzzles have used the technique to great effect. And it’s something that you can visualise without writing down candidates or any extra notation, although sometimes the eliminations can be tricky to see in much the same way that box reduction eliminations can be hard to see.
I do sympathise with the sentiment on puzzles that just happen to require colouring or y-wings to finish off the last 15 numbers. Sometimes you have a puzzle which happens to come out uniquely, but one particular technique seems out of kilter with the rest of the puzzle. I’d be interested to hear what you think about this puzzle:
http://tcollyer.blogspot.co.uk/2013/03/friday-puzzles-198.html
It starts and ends with a flurry of placements, but requires a little colouring in the middle of the solve. I ended up explaining how colouring works to some people in my old office, visually eliminating the 4th corner of a “rectangle.” Granted, these are phd mathematicians, but the idea seemed surprisingly intuitive to them.
In more generallity, I think the distinction that needs to be made here is between solving for pleasure and for competition. I think the informal line I’d draw between the two is if spotting and applying a hard technique requires you to write in the full candidate lists for all (or most) of the unsolved cells. I’ve spotted (albeit presumably unnecessary) and used finned x-wings/swordfish whilst “speed” solving on many occasions, for example.
And to be honest, when not solving against the clock there is some satisfaction to be had in trying to deploy the generalisations of colouring and y-wings in the more brutal puzzles. I think the informal line I draw there is when applying one hard technique only eliminates candidates which then set up another hard technique. That’s when things start getting a little tedious in my book. On the other hand, if using a hard technique yields the placement of a number, moving the solve along, then that’s the kind of satisfying thing I don’t mind when the stopwatch has been put away.
You bring up an important subtlety that might flavor my opinion of some of these steps: they feel different when they give you a digit than when they give you just another candidate elimination for something else. I haven’t run into many sources that highlight colouring at the right stage or have it give a sure digit (exception only of diagonal sudoku where I use it a lot). The Saturday puzzle actually set up a tension where it wasn’t just one sure digit but several that would arise in C2 once you got the Y-wing. Which definitely made me feel better about using it even though I expected some solvers to have FoxFireX’s sense of frustration for having such a step.
I agree about simple colouring that it can be easier to work with, only if I could pick the right candidate for applying that technique on,without falling into bifurcation .I believe this method can be possibly used when only one or two different digits remain unplaced.
I need to put emphasis on a word in one of your sentences:
“When I can solve a puzzle in ink, without erasures, with all deductions either positive or negative coming from visualization in my head and not making scratch-work on the paper, the puzzle is solvable by logic.”
When YOU can solve it. But last I checked, you were consistently one of the top solvers in the world.
That means that the things YOU can visualize in your head are things that many people will need to visualize on paper. Sometimes mental visualization can be improved by extensive practice, but I think some natural spacial ability is necessary too.
Like having a good sense of direction, natural spacial ability is something that some people just don’t have.
All of this said, I understand what you are getting at with your standard. I prefer to solve puzzles in ink, too! But when one of us here says that we had to guess at a puzzle, we don’t mean that the puzzle didn’t fit your standard – we just mean that the puzzle exceeded our own personal capacity to visualize the solution. (Or in other words, “That was a hard one!”)
Your point is well-taken, but I’ll emphasize something people don’t get about speed solvers until watching them for awhile. It is not that we see so many more steps than other solvers. We just see them much faster, and have gotten experienced at finding the “signal” without losing as much time. There is no “super secret Slitherlink pattern” I know that others don’t, for example. I’ve gotten good at using notation in sudoku puzzles to be faster at them, but there is nothing unique about the approaches I use there either. If you take a video of a sudoku solve of mine, and slow it down by some factor, it will in many cases look like videos from other solvers and you can explain each digit placed.
That said, there is a very wide range of puzzles here. And some, like the “isodoku”, do challenge visual perception in unusual ways. Others challenge arithmetic capability in unusual ways. And so on. We all have our good and bad areas and I’m not suggesting people only use pens. We should all solve puzzles the way we want to maximize the fun we get from them; I have fun on puzzles that have “fair” solutions and this is what I’m focused on posting.
A couple things I found intersting/important in this conversation. For those of us in the expert/master categories, seeing more complex patterns is where we can actually keep up with (occasionally surpass?) the top solvers, particularly on variants. In fact the most depressing moment for me came after watching Thomas’ Youtube series a while back and realizing there really wasn’t anything I was missing – I just wasn’t (and will never be) that fast.
While it is true that the best solvers don’t have “super secret techniques” compared to other good solvers, I am not sure whether the same can be said when compared to a not-so-good solver, or one that is new to a genre. I have never heard of the XO technique for in/out slitherlink in WPC 2009 before I was told about it by my teammates. Of course, it was my fault for not knowing/practicing the OAPC (it was my first WPC), but I think my point still stand.
Sure. And the point of my article is that the puzzles here will use deducible techniques and not guesswork. Not all solvers may know these but persistent ones might learn something by working through the puzzles. Or, if they do get stuck, asking here in the comments for assistance (which can indicate to me it is a good Ask Dr. Sudoku topic). Most puzzlers are really open in helping discuss how to solve a particular puzzle, again because there isn’t a real benefit in holding onto “super secret techniques” as there aren’t any.
After working at Saturday’s Sudoku for a while, I can definitely say that this is the case.
I hit expert times almost always and master times frequently, but I am solidly a “hobby” puzzler and don’t consider myself as a competitive one. I visit puzzle websites to solve puzzles. I don’t habitually read about techniques, and I had never heard of a “Y-wing.” Until now, I’ve developed all of my own solving strategies. Obviously at this point, Sudoku-related strategies have not come naturally to me. (Oddly, I seem to be much better at Isodoku – or perhaps others are worse.)
I have no idea what “X-wing” or “swordfish” mean either, while we’re at it. I could go look them up, but it almost feels like cheating.
Wait, that was a Y-Wing? I’m mystified that this puzzle was given a “Woah!!!” rating in Sudoku Tiger; Y-Wings, as unfamiliar as I am with them as a technique I’ve never had to be on the lookout for in a Nikoli puzzle, are definitely a technique listed in the Help file. I’ve become very well-versed in X-Wings and Swordfish, but Y-Wings. . . phew.
Okay, this is about six months late, but I recently started going though the entire GM Puzzles site from the beginning! I do every puzzle twice: First I speed solve, making extra marks and doing what I can to get the solution as fast as possible. Then I solve it again “logically”, writing in only the pieces of the final answer and appreciating all the logical deductions.
I’m having a great time with all the puzzles!