Eighth in a series with puzzle solving tips. This time with advice on battleships puzzles, particularly missing clues and subs.

Solving Battleships is an odd experience for me. I think I want to enjoy them, but I’m not sure I ever really do very much. See, they were the first logic puzzle type I ever grew to love. But that means they also became the first logic puzzle type to bore me, and I’ve now been in the “bore me” stage for over half my life. And there is so much sameness in the Battleships you can find in the world right now. ~99% are randomly generated, ~99% give all of the outside clues which limits the challenge, ~99% solve by placing the largest ship(s) in the only possible spots and being good at bookkeeping of seas afterwards. As a member of the puzzling 1%, I am looking for something more. This week I tried to vary the formula a bit to make some more interesting — or at least different — puzzles.

Because missing clues aren’t common, the “add to 20” rule isn’t known by everyone either. I tried to introduce this in the most instructive but least interesting way in the first puzzle this week missing clues, the Thursday Battleship Sudoku. Since the bottom columns are already deterministically set as in the image, my obfuscation of removing some clues wasn’t actually doing anything but testing if you knew the “add to 20” rule. At best, I hoped this presentation would serve to teach the rule to new solvers even if it was well-known to everyone else.

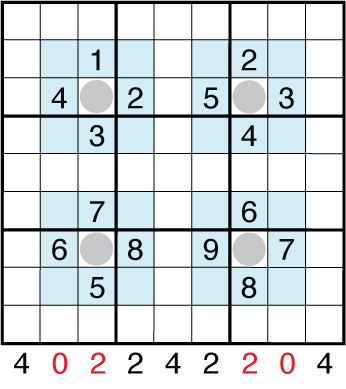
But the puzzle hides a different kind of deduction afterwards which was meant to be more interesting. In most puzzles, submarines are an afterthought. They are the last ships placed, to allow a row or column to get to the right tally, but don’t figure much into the solve.

Here, I give all the subs at the start and the usual thinking is thrown off. Now parity and grid packing become really critical. The 2- and 4- unit ships have a lot of choices but the 3-unit cruisers cannot be in the first or last column. They also can’t be vertical in the middle as that will keep you from filling column 4 and 6 without overfilling column 5. So you have only three spots for the cruisers (but many for the battleship and destroyers). Here, the numbered clues from the Battleship Sudoku will get you started by sorting out exactly which 2 of these 3 options are used.

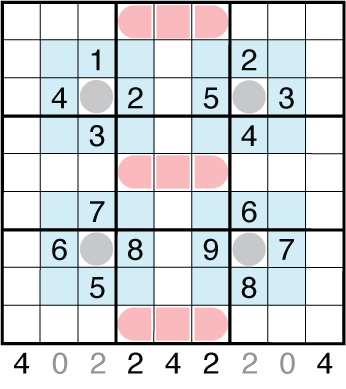
Finishing the puzzle requires finding, from numbers, where the battleship can go. The “4” and “6” in the middle-right box eliminate all options that sit near the middle of the column, and other numbers eliminate the remaining options. It goes in column 1, and once you place a 6 from sudoku solving over there you can spot that ship, and then the last cruisers, more quickly.

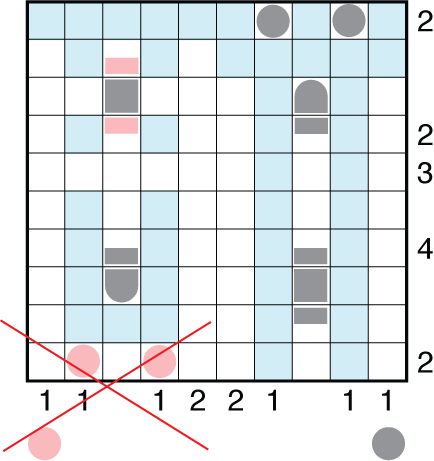
But this is a lesson on missing clues and submarines so I wanted to talk about the Friday puzzle too. Basic starting marks should get you to this state (my notation on paper is not exactly what I display here with half boxes, but visually this is cleanest). The count of 10 and 7 missing from columns/rows is not as easy to use yet, but is worth noting.

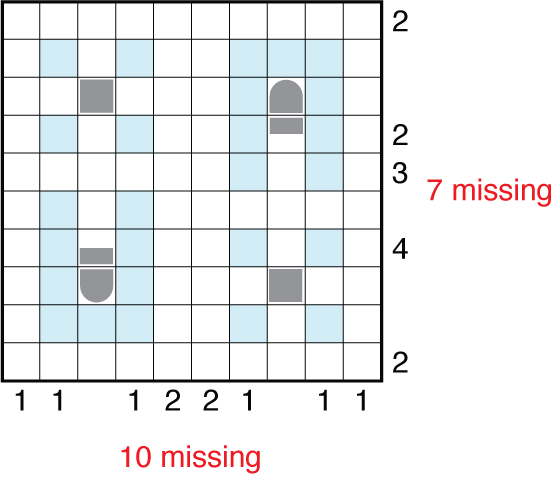
Most battleship puzzles are solved logically by finding rows/columns with the highest degree of tension — namely, where there need to be a lot of ships or not many ships and the current solving state limits the degrees of freedom. The highest tension spot in the starting grid is the 4 in row 7. With the vertical or horizontal large ship just beneath it, a good solver will quickly see that there is no horizontal option as that eliminates 3 of 5 remaining unmarked cells and that makes getting to 4 total ships in the row impossible. The consequences of this deduction are to place three submarines into the grid. You may not know where they all go yet, but marking your paper like this will be useful.

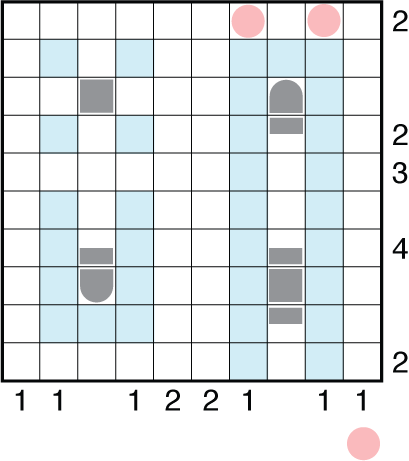
This grid has a lot of symmetry, and one thing learned in the last step is that a vertical ship from the square clue forces two submarines in the first row. Well, the same situation in the third column presents itself. A vertical ship there would force two more submarines in the bottom row and a third somewhere in the first column. But you can’t have six submarines in the grid.

Running out of submarines forces you to place the ship in horizontally. (Some other options exist to deduce this too, but this is how I constructed the puzzle to have something learned earlier in the solve come up again). Now, as the horizontal ship places many more segments into unmarked rows, this is a good time to revert to “add to 20” mode. You’ll find 7 segments are now in the unmarked rows, so all ships in those unmarked rows are now accounted for. The horizontal ship you just placed is a 3-unit cruiser.

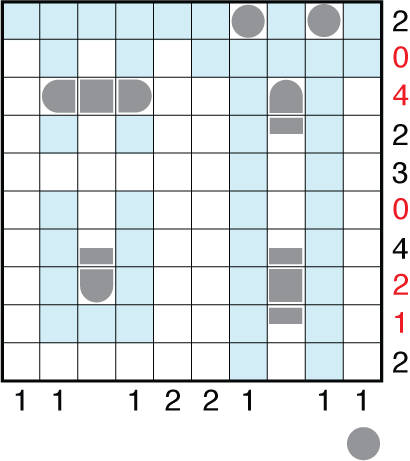
And the rest is much easier from there. I could have made the puzzle much harder by leaving out or adjusting some of the row clues.

Writing Battleships is an odd experience for me too. All my rules and info pages start with the line “A Grandmaster XXXXXXX will have a unique solution that can be reached by logic alone.” Battleships is the one style where I know my solvers may not approach the puzzles with a logical solution in mind at all, even telling them this fact up front. For many, Battleships has become a brute-force branch-killing heuristic that begins with the 4-unit battleship and nothing else is allowed! I was surprised when my most experienced Battleships tester, for both Monday and Wednesday, reported going to guessing or being unable to prove uniqueness from his solving path. One solver here posted on Friday a very quick result that included guessing the location of one ship and then stated I had failed to correctly time the Friday puzzle despite six testers, none faster than 3:50 and most closer to 10 minutes. I know I can write interesting Battleships. But I’m not sure I can make my audience solve them as intended. And when someone gets lucky, that does not make the puzzle easy. That makes them lucky.